This is an old revision of the document!

Dr. Philippe H. Trinh
Lecturer (Assistant Professor) in Applied Mathematics
Department of Mathematical Sciences
University of Bath
Bath, Somerset, UK
p.[my-last-name]@bath.ac.uk
Mathematical Institute Profile
Collaborators and students
+ Curriculum Vitae (2016)
- You might also be interested in learning a bit about what I do and the wonderful people I get to work with.
14 September 2017: Congratulations to graduating and continuing research students
This comes a bit late as we are only two weeks away from a new academic term, but I wanted to pause and congratulate many of the successful research students from the 2016-2017 year.
- John Fitzgerald completed his outstanding Part B Extended Essay on Complex ray theory, exponential asymptotics * applications to free-surface flow and earned one of the highest essay marks of the year. He will continue on to do his Part C dissertation this year.
- Yyanis Johnson-Llambias completed his Part C dissertation on Complex singularities of the finite-depth Stokes waves and will begin a doctoral degree in mathematics at Bath University this month.
- Thomas Chandler completed his Part C dissertation on Complex singularities near the intersection of a free-surface and a rigid wall, which also took home the Gibbs prize. (And so concludes two very special years working with Tom, who also completed his Part B Essay with me the prior year). Tom will continue at Oxford as a DPhil student in mathematics.
This coming academic year will bring a lot of new exciting undergraduate research students, both new and old. Stay tuned for announcements!
17 June 2017: The Oxford-Cambridge Woolly Owl
Yesterday, we sent our team of seven students to compete against Cambridge in the Applied Maths Meeting (aka the Woolly Owl). This is a bienniel competition between Oxford and Cambridge graduate students to claim the prize of the Woolly Owl, a plush toy knitted by a tea-lady in the Maths Institute many years ago. The winner of the competition would be allowed to retain the owl for the next two years until the next clash.
The history of the meeting stretches back to 1983. More on the meeting later, but here is a photo of Emeritus Profs. John Ockendon from Oxford and Herbert Huppert from Cambridge who agreed that they were the joint founders of the meeting.

25 May 2017: A tax on those who can't do maths
It's said that playing the lottery is akin to imposing a tax on those who cannot do mathematics. However, there are plenty of real-life situations where it becomes difficult to gauge whether or not you are getting a good deal. Issues of real-estate, investment, and mortgaging is one of those situations.
Here's a typical situation that will be familiar to a lot of our readers. You would like to take out a mortgage of a certain amount, let's say $L = L_0$. Currently, Halifax has a deal where they will charge you a fixed rate of $r_1 = 2.11\%$ interest on the first $t = n_1$ months. For the remainder of the time, up to $t = n_e$, they will charge the variable rate, which for simplicity we assume to be at $r_2 = 3.74\%$.
Now when you fill out the details of the mortgage on their calculators, it will indicate how much you should be paying back per month, and this takes the form of a fixed amount $m_1$ for the first period and $m_2$ for the second. The question is then: how are $m_1$ and $m_2$ determined? Clearly, if $m_1$ is very large, then this is typically in your best interest, as you profit from the better interest rate. Is the rate they set in your favour or theirs?
This turns out to be a question of recurrence relations. Let $L_n$ be the current loan amount in the nth month. During the first period, $0 < n < n_1$ we can verify that \[ L_n = L_{n-1}(1 + r_1/12) - m_1, \]
where $r_1 = 0.0211$ is the interest rate and it is assumed to be compounded monthly. From this, it follows that \[ L_n = k_1^n L_0 - m_1 \left(\frac{1 - k_1^n}{1- k_1}\right), \]
where we have set $k_1 = 1 + r_1/12$. In the same vein, we reason that in the second period, where $n_1 < n \leq n_e$, it follows that \[ L_n = k_2^{(n-n_e)} L^* - m_2 \left(\frac{1 - k_2^{n-n_e}}{1- k_2}\right), \]
where we have set $k_2 = 1 + r_2/12$. The key parameter here is the value of $L^*$, which is the loan amount that exists in the changeover month, $t = n_1$. By solving the above equations for $m_1$ and $m_2$, then these fixed monthly payments can be determined as a function of $L^*$ and all the other parameters of the problem.
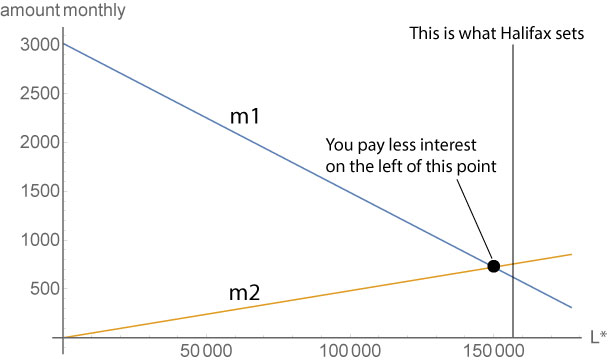
As a test, I found that Halifax was quoting me monthly figures of $m_1 = £620.87$ and $m_2 = £755.81$ for a loan of $£176,999.00$. This is for the initial fixed period of $n_1 = 62$ months and then the remaining period stretches to month $n_e = 396$. Below is a graph of the two fixed monthly payments as a function of the changeover amount $L^*$.
Based on the image, you see two things. First, there is a critical point of intersection where you would pay exactly the same every month, and where $m_1 = m_2$. This point occurs at $£723.432$. To me, it would seem sensible to simply charge this fixed amount for the duration of the mortgage. Of course, people will remortgage depending on the change in the interest rates, but why not require this value?
The second point is that the changeover amount that Halifax imposes is instead on the right side of the intersection. Hence it requires a smaller initial monthly payment but a larger later payment. Because the total amount of interest paid increases (linearly) as you decrease $m_1$, this is in Halifax's favour. The difference amounts to around £6,712.
What this certainly indicates is that it's not enough for you to simply consider the duration of a fixed-term mortgage, but there are often sneaky calculations behind the scenes that may be suboptimal for you if you go with their repayment scheme.
30 January 2017: On reduced models for gravity waves generated by moving bodies
I'm happy to announce a recent paper published in the Journal of Fluid Mechanics. There is an interesting story behind this paper.
 (Left) Ernie Tuck (1939–2009) (Right) Marshall Tulin (1926–)
(Left) Ernie Tuck (1939–2009) (Right) Marshall Tulin (1926–)
Since around 2007–2010, I'd often play with certain reduced models for studying gravity wave generation by two-dimensional bodies. These reduced models you can derive using some more modern techniques in asymptotics, but actually I had noted that in the early 90s, the late Ernie Tuck from the University of Adelaide had published some thoughts on similar reductions. I had thought that this was the end of the story.
A few years ago, I spotted a curious question that was written in a transcription of audience questions in a conference where Tuck had presented his research (in fact, such transcriptions are quite rare in this day and age). Marshall Tulin, another famous hydrodynamicist from Santa Barbara, had asked the following question:
“Isn't it true that the two dimensional wavemaker problem can be presented in terms of an ordinary differential equation in the complex domain, at least to some higher order of approximation?”
Tuck had replied that he didn't know the answer, and the matter was apparently left at that. However, Tulin's question was certainly a deep one, and the fashion in which it was asked led me to believe that Tulin had been on a similar trail even before 1991. But contacting Tulin was no easy feat; though he was listed as Emeritus at Santa Barbara, my first email had bounced. In the end, I managed to locate a personal email, and so I sent off a letter asking if he could fill me in on what his intention was behind the question.
Tulin was quite pleased to have been asked for more details (as it had been over two decades since that conference!). He told me that he had, in fact, published a report in 1983 for the 14th Symposium on Naval Hydrodynamics where he laid out a particularly involved reduction of the water wave equations.
He explained that nobody had really picked up on the 1983 paper (1 current citation!), even though there were a series of questions he had asked and a series a results he had presented that had seemed of some importance. He encouraged me to look up the manuscript and close the chapter, if I could.
And so I did. The result is this most recent paper.
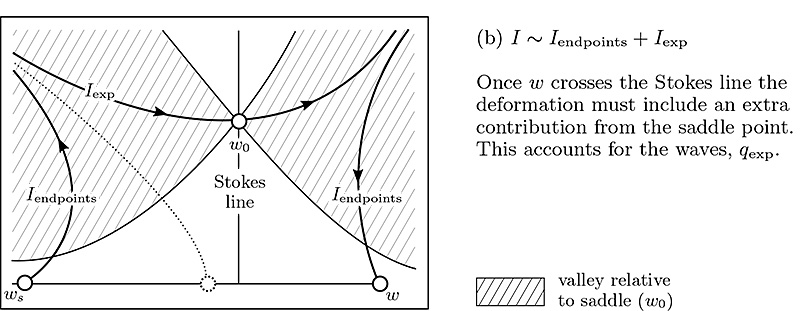
8 September 2016: A topological study of gravity free-surface waves generated by bluff bodies using the method of steepest descents
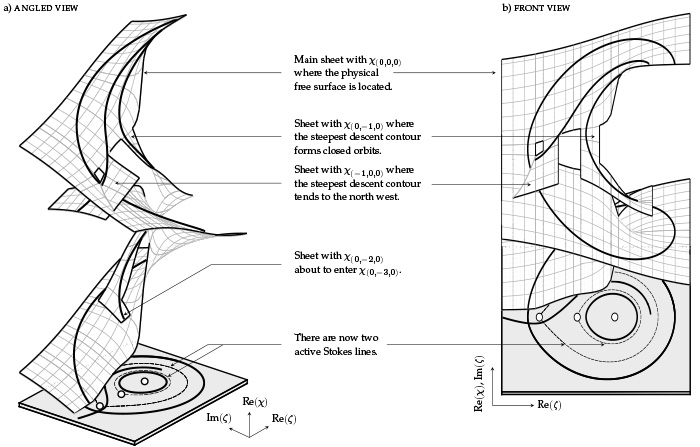
This paper, now published in the Proceedings of the Royal Society A (PRSA) has a few interesting distinctions. It's the first paper I've published in PRSA—but hopefully not the last as it's certainly a strong journal with an illustrious history. It's the first solo paper I've published. And it has the longest title of any other paper I've worked on.
In any case, it's a paper where I explore exponential asymptotic techniques for free-surface flows (now well known) from a slightly different viewpoint. It turns out that the situation of gravity waves permits the governing equations to be re-formulated in a particularly simple way: that of a first-order nonlinear differential equation. In this paper, I show how the differential equation is studied using steepest descents. What results is a visual and beautiful way of understanding wave-structure interactions through a correspondence with the topology of certain Riemann surfaces (seen above).
You can download a copy of the paper here. This paper technically forms Part 2 of a two-part series of which the first is still in review.
01 June 2016: New singularities in Stokes waves
I'm happy to announce the publication of a paper in collaboration with Samuel Crew (Lincoln College, Oxford). In this paper, we revisit the classic problem of a periodic wave travelling without change of form, which was first considered by Stokes in the late 19th century.
Interestingly, there are still several unanswered questions regarding this canonical example of a water wave. Some of these questions concern the existence of the singularities in the complex plane, along with their behaviour as the wave steepens. You can read the paper here.
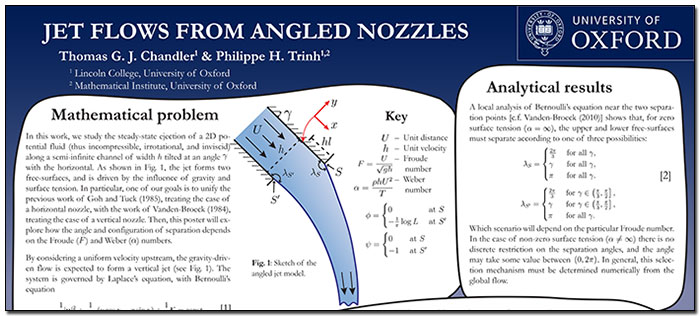
18 May 2016: Jet flows from angled nozzles
A late congratulations to second-year student Tom Chandler (Lincoln College, Oxford) for successfully presenting his poster Jet flows from angled nozzles at the British Applied Mathematics Colloquium 2016 that took place last month in Oxford. Tom's work studies the situation of fluid ejected from an angled nozzle and driven by gravitational forces. It turns out that there are some rather non-trivial issues concerning the angle that a liquid separates from a solid, and this deals with the interplay between geometry, surface tension, and gravity. Tom's poster forms part of his third year dissertation project and will continue to a summer research project at the Mathematical Institute.
Jan 2016: Spot patterns on the surface of the sphere
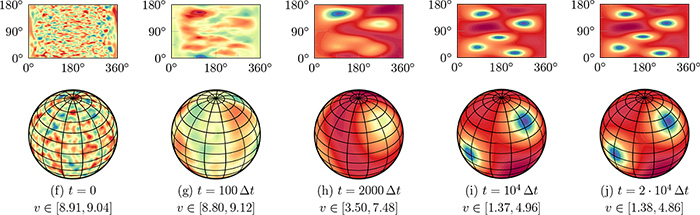
I'm happy to announce the publication of my paper in the journal Nonlinearity with Michael J. Ward (University of British Columbia) on localized spot patterns on the surface of the sphere. In this paper, we develop the detailed asymptotics that describe the slow dynamics of spot patterns modelled by a system of reaction-diffusion equations. The interesting twist is that when the patterns occur on a surface of non-zero curvature, the methodology must account for higher-order terms due to the changing geometry. It is a wonderful paper with some beautiful mathematics and beautiful pictures.
June 2015: Fluids and elasticity in France
I'll be attending the Fluid and Elasticity 2015 conference, from June 22-24 in Biarritz, France, and presenting some joint work with Stephen K. Wilson (Strathclyde University) and Howard A. Stone (Princeton University).
May 2015: Two new papers published
I'm happy to announce the publication of two new papers. The first paper is published in Nonlinearity and is on the topic of developing exponential asymptotics for problems with coalescing singularities (motivated by the study of ship waves, above left) with Jonathan Chapman (Oxford). The second paper, published in the Journal of Fluid Mechanics, and collaboration with Weiqing Ren (National University of Singapore) and Weinan E (Princeton) seeks to explain the importance of distinguished limits in the classical contact line problem. Both papers can be downloaded from the research section.